Fractical is a simple fractal viewer that can paint the Mandelbrot and Julia sets.
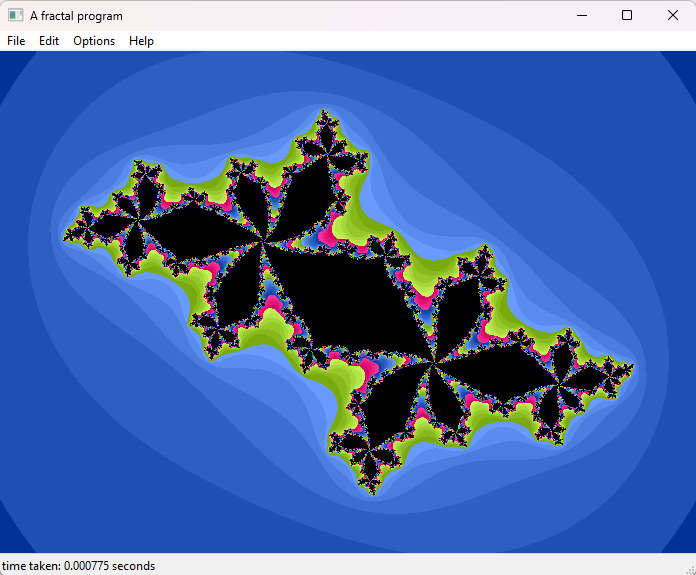
A fractal is a geometric shape containing detailed structure at arbitrarily small scales, often exhibiting strong self-similarity. Which is a fancy way of saying crazy-looking acid inspired fever dream math stuff. Benoit Mandelbrot coined the term fractal in 1975 to describe these types of objects and they became really popular in the 1980's when computer graphics became powerful enough to draw them. I, like many others, became obsessed with them and tried my hand at making a fractal viewer. This was also a fun way to teach myself C++ and GUI programming in WxWidgets.
The program itself is simple enough. It can draw the Mandelbrot set and various Julia sets with a given starting point. You can zoom in and out and move around, and you can also change the number of iterations for greater level of detail. What does any of that mean? I'm glad you asked!
One of the earliest examples of fractals in mathematics were discovered by Gaston Julia in 1918,
and are called Julia sets. The defition is simple. Take a function like this one:
where f is a function of complex numbers and c is a complex constant. Then iterate this function,
One of two things happens: Either the sequence of numbers grows to infinity, or it stays within some
bounds. The set is defined as the numbers that stay. Each choice of the constant c will yield a different
Julia set.
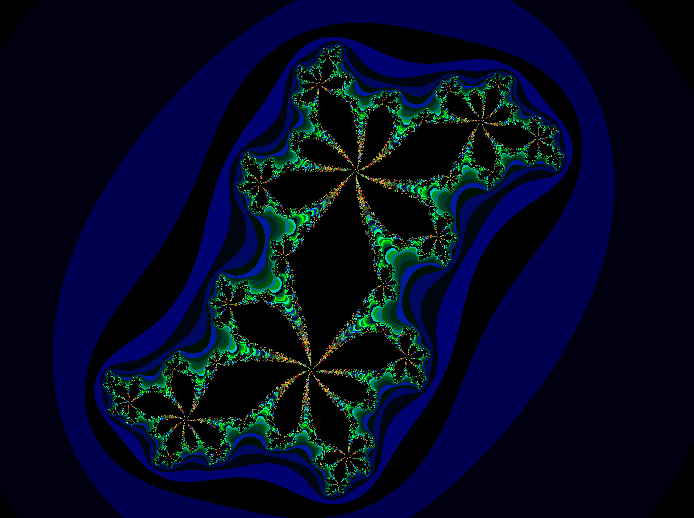
Julia sets can be connected:
or disconnected.
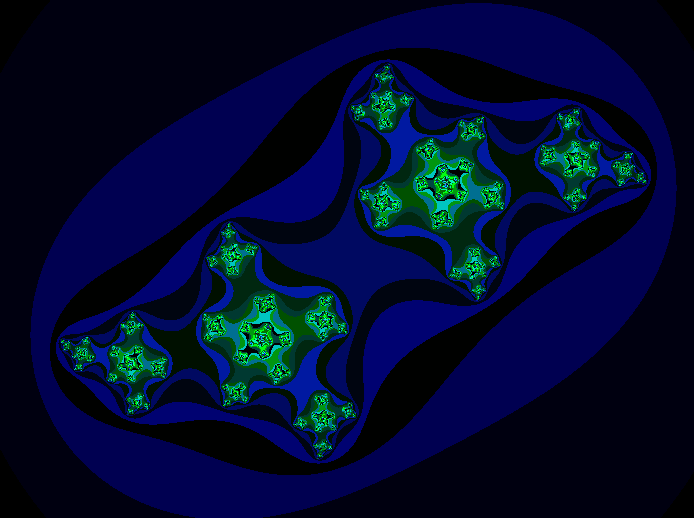
Without going into too much detail about what that means mathematically, the pictures should give an idea.
A thing to note is that a connected Julia set will include the origin point, z = 0+0i, whereas a
disconnected set will not.
So Mandelbrot had the idea of making a kind of a map of all the Julia sets. To see where all the connected
Julia sets are, and the disconnected ones. Doing that turns out to be relatively easy: Simple fix z = 0+0i
and then choose different values for the constant c. Actually, let c range from -1-i to 1+i, so that c is now
the starting coordinate. Iterate as before and note that those c-values that stay within bounds correspond to
connected Julia sets. This is the Mandelbrot set, and it looks like this:
Pretty crazy, right?