Some more stuff about fractals. This post is mostly based on the book "Fractals Everywhere" by Michael F. Barnsley. It's also the basis of my bachelor's thesis in mathemathics which you can find right here:
We are mostly dealing with something called Iterated Function Systems, or IFS for short. It might sound complicated, and it kind of is. But on the other hand look at the pretty pictures!
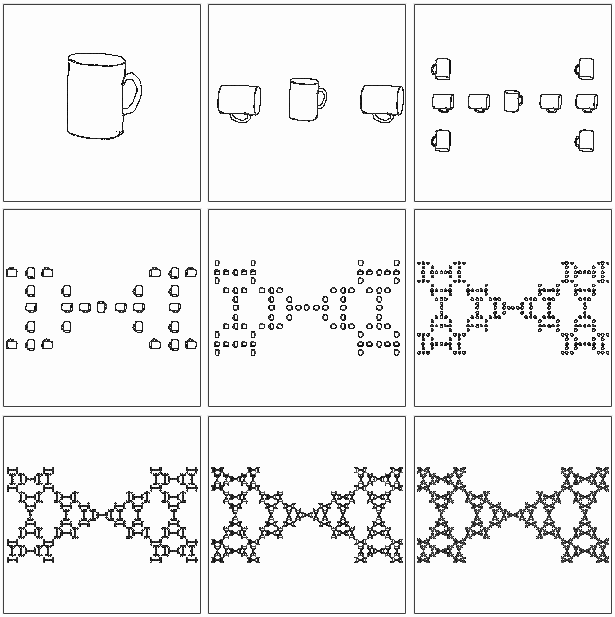
These are all examples of IFS's. The idea here is to take any set of points (i.e. a picture) and
perform a series of linear operations on it. What that means is we're allowed to stretch the picture,
move it and rotate it (Actually the stretching has to be negative for out purposes, i.e. instead
of stretching we shrink. We call this a "contractive" linear mapping). We then do this repeatedly.
The result could look something like this:
We started with a random set of points (here a picture of a coffee cup) and applied three linear
operations on it, i.e. shrink by 50%, move to the middle, then also shrink by 50%, rotate by 90° to the
right and paste it to the left and to the right.
The first two pictures really explain what's going on if you zoned out just there. The rest of the pictures is just repetitions of the same thing, eventually leading to the picture on the bottom right. Of course, after a finite repetition of this, we still have a coffee cup structure essentially, the coffe cups just happen to get smaller and smaller. But the limit set of this operation is defined to be the points that happen to be limits of sequences defined by each starting point subjected to the IFS. I.e. there are no coffee cups in the actual limit. The limit is called an "attractor" for the IFS. An alternative definition is the set of point that is "invariant" under these operations, which is to say the only set of points that doesn't change when applying the IFS.
Again, "applying the IFS" just means to do the three things we decided in the beginning, which is pictured in the first two pictures up there - shrink, rotate, move to the left and right. And the magic is that it doesn't matter what we started with, any picture- even a single point - will always converge to the picture at the end. This is a result of The Collage Theorem by Michael Farnsley.
Here is a simple python program which I used to draw these pictures. It's currently set to draw the Sierpinski triangle which is easily drawn using an IFS. This program uses numpy and pygame. You can draw on the screen with the mouse and then press any button to apply the IFS, which is defined at the top.
Recently updated to run with python version 3.10. Uses pygame and numpy. Basic usage: Draw on the screen using the mouse and then press any key to apply the IFS defined at the top of the file. Do this repeatedly to see the fractal emerge. Press ESC to quit, and F9 to take a screenshot.